競馬における能力比較には「偏差値」を用いた方が良い理由

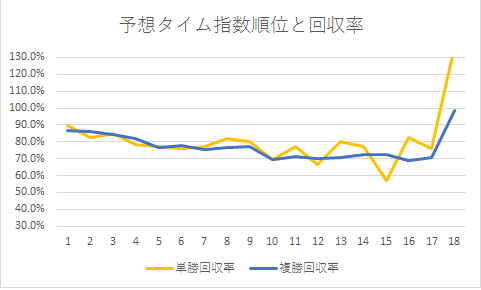
前回「馬王Ｚの予想タイム指数は使える指数なのか」を検証しましたが、その際は出走馬の中での横比較をするために「予想タイム指数の順位」を使用しました。

馬王Ｚの予想タイム指数の実力

2018年8月17日

しかし、「順位を用いるとメンバー中の序列関係は比較できるものの、各馬の指数値の開き具合は計測できない点が欠点だ」という趣旨の内容を最後に書きました。

今回はそのようなスピード指数を比較する際の課題への対策について考えたいと思います。

例えば５頭立てのレース【例1】【例2】があり、各レースの出走馬のスピード指数が以下の通りだったとします。

2つの例はどちらもスピード指数順位の並びが「Ａ馬→B馬→C馬→D馬→Ｅ馬」の順となっていますが、それぞれの能力分布は全く異なります。

例1は上位３頭が拮抗しており逆に下位２頭が離されている状態、例2は上位１頭が抜きん出ており他は団子状態という構図になっています。

同じ指数１位でも信頼度は例2の方が高いと考えられますし、逆に指数2位の馬に対する期待度で言えば例1の方が上でしょう。

指数を順位だけで比較しようとするとこのような指数値の散らばり具合がうまく表現できないのです。

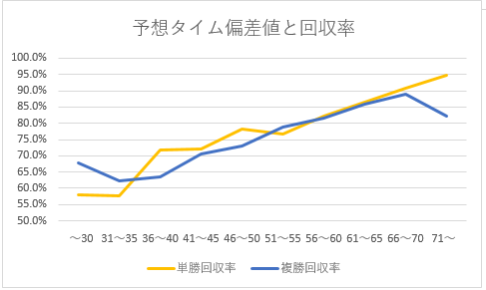
そこで、このようなスピード指数系のデータを比較するときは「偏差値」を使うことをおススメします。

偏差値なんて学生時代のテスト以来は使ったことがないという人もいそうですが、「自分のテストの出来具合」を表現するのに偏差値がわかりやすかったように、競馬でも「指数値のレベル感」を表現するのにこの偏差値が打ってつけなのです。

ここで、「偏差値の計算の仕方なんて知らない、あるいは覚えてない」という人のために、計算手順を説明しておきます。

偏差値は以下の3ステップで計算できます。

１．平均値を計算する

例1のケースだと以下の値になります。

２．標準偏差を計算する

数学嫌いな人には標準偏差という言葉は耳慣れないかしれませんね。

標準偏差というのはデータの散らばり具合を表す数字です。

競馬のレースで言えば、各馬の力が拮抗しているのか、それともバラバラなのかといったものを測る尺度です。

計算方法は、各データについて「1」で求めた平均値の差を２乗し、さらにそれらの平均を取ってその平方根(√)を求めるというちょっと複雑なものになります。

具体的には以下のように求めます。

３．偏差値を計算する

最後に偏差値を求めます。

これは各データと平均値との差を標準偏差で割り、それを10倍して50を足したものです。

例えば例1のＡ馬の偏差値は次のようになります。

これと同様に例1と例2の全馬の偏差値を求めると以下の通りとなります(見やすさのため少数第一位を四捨五入しています)。

偏差値は50が平均なので、それと比較することで各馬がどれくらい強いのかイメージがしやすくなりましたよね。

私のように勉強ができるかどうかを偏差値で比べられていた世代にとっては、「偏差値70は凄い、偏差値30は悪い」と直感的にわかると思います。笑

また過去データを集計する際にも、「スピード指数が90の馬」といったまとまりで成績を調べるよりも「スピード指数の偏差値が70の馬」の成績を調べる方が適切であることもおわかりいいだけるでしょう。

例1と例2のケースではいずれも指数１位馬の指数値は90ですが、各レースでの評価は全然異なるので、これを集計したところであまり意味はないですからね。

このようにスピード指数などの能力系指数は偏差値で比較すると適切なデータ分析ができることが多いので、もしあなたがこれまで競馬で偏差値を使うという発想を持っていなかったとしたら、ぜひ一度試してみて下さい。

なお、世の中の指数にはすでに偏差値化した数値を配信しているものもありますので、わざわざそれをさらに偏差値化するような無駄なことはしないようご注意下さい。

さて、偏差値化のメリットがわかったところで、次回以降は馬王Ｚの予想タイム指数をはじめ、その他のソフトのスピード系指数について偏差値化してその有効性を確認してみたいと思います。

【次の記事】

馬王Ｚの予想タイム指数を偏差値で比較してみる

2019年3月16日